追記: xymatrixによる可換図式のテンプレート

これまでxymatrixによる可換図式のテンプレートを書いた。その一連の記事は
Part I
Part II 
Part III
である。これらは少し読みづらいと思う。こちらの記事の方が見やすいと思う。適宜参照しても構わない。
Part I
(0)

%(0): 基本
\documentclass{article}
\usepackage[all]{xy}
\usepackage{amsmath, amssymb}
\begin{document}
\[
\xymatrix{
A\ar[r]^f&B
}
\]
\end{document}

(1)

%(1)
\begin{equation}
\xymatrix{
A\ar[r]^-{f}&B
}
\end{equation}

(2)

%(2)
\begin{equation}
\xymatrix{
A\ar[r]_-{f}&B
}
\end{equation}

(3)

%(3)
\begin{equation}
\xymatrix{
A\ar[r]|f&B
}
\end{equation}

(4)

%(4) Left Arrows
\begin{equation}
\xymatrix{
A&B\ar[l]^-{f}_-{g}
}
\end{equation}

(5)

%(5) Vertical Arrows
\begin{equation}
\xymatrix{
A\ar[d]^-{f}_-{g}\\
B
}
\end{equation}

(6)

%(6)
\begin{equation}
\xymatrix{
A\\
B\ar[u]^-{f}_-{g}
}
\end{equation}

(7)

%(7) Unique Arrows
\begin{equation}
\xymatrix{
A\ar@{.>}[r]^-{^{\exists !} f}&B
}
\end{equation}

(8)

%(8) Inclusion Maps
\begin{equation}
\xymatrix{
A\ar@{^{(}->}[r]^-{f}&B
}
\end{equation}

(9)

%(9) Monomorphisms
\begin{equation}
\xymatrix{
A\ar@{>->}[r]^-{f}&B
}
\end{equation}

(10)

%(10)
\begin{equation}
\xymatrix@M=8pt{
A\ar@{>->}[r]^-{f}&B
}
\end{equation}

(11)

%(11) Epimorphisms
\begin{equation}
\xymatrix{
A\ar@{->>}[r]^-{f}&B
}
\end{equation}

(12)

%(12) Identity Arrows
\begin{equation}
\xymatrix{
A\ar@{=}[r]^-{1_A}&A
}
\end{equation}

(13)

%(13) Isomorphisms
\begin{equation}
\xymatrix{
A\ar[r]^-{\simeq}_-{f}&B
}
\end{equation}

(14)

%(14) Assignments of Elements
\begin{equation}
\xymatrix{
x\ar@{|->}[r]&y
}
\end{equation}

(15)

%(15) Natural Transformations
\begin{equation}
\xymatrix{
F\ar@{=>}[r]^-{\tau}&G
}
\end{equation}

(16)

%(16)
\begin{equation}
\xymatrix{
\textbf{C}\ar@/^18pt/[rr]^-{F}\ar@/_18pt/[rr]_-{G}\ar@{}[rr]|{\Downarrow^\tau}&&\textbf{D}
}
\end{equation}

Part II
(18)

%(18) 2つの射
\begin{equation}
\xymatrix{
A\ar[r]^-{f}&B\ar[r]^-{g}&C
}
\end{equation}

(19)

%(19) 合成射(Compositon) Case I
\begin{equation}
\xymatrix{
A\ar[r]^{f}\ar@/^18pt/[rr]^{h}&B\ar[r]^-{g}&C
}
\end{equation}

(20)

%(20) 合成射 Case II
\begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar@/^18pt/[rr]|h&B\ar[r]^-{g}&C
}
\end{equation}

(21)

%(21)  合成法則(The Composition Law)
\begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar@/^18pt/[rr]^-{g\circ f}&B\ar[r]^-{g}\ar@/_18pt/[rr]_-{h\circ g}&C\ar[r]^-{h}&D
}
\end{equation}

(22)

%(22) Case I: 0.5ex
\begin{equation}
\xymatrix{
A\ar@<0.5ex>[r]^-{f}\ar@<-0.5ex>[r]_-{g}&B
}
\end{equation}

(23)

%(23) Case II: 0.8 ex
\begin{equation}
\xymatrix{
A\ar@<0.8ex>[r]^-{f}\ar@<-0.8ex>[r]_-{g}&B
}
\end{equation}

(24)

%(24) 同型射(Isomorphisms)
\begin{equation}
\xymatrix{
A\ar@<0.5ex>[r]^-{f}&B\ar@<0.5ex>[l]^-{f^{-1}}
}
\end{equation}

(25)

%(25) Case I: 1.5 ex
\begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar[d]_-{h}&B\ar[dl]^-{g}\ar@{}@<-1.5ex>[dl]|{\circlearrowright}\\
C
}
\end{equation}

(26)

%(26) Case II: 2.0 ex
\begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar[d]_-{h}&B\ar[dl]^-{g}\ar@{}@<-2.0ex>[dl]|{\circlearrowright}\\
C
}
\end{equation}

(27)

%(27) Case III: 2.5 ex
\begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar[d]_-{h}&B\ar[dl]^-{g}\ar@{}@<-2.5ex>[dl]|{\circlearrowright}\\
C
}
\end{equation}

(28)

%(28) 別の回転射(Another cicle arrow)
\begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar[d]_-{h}&B\ar[dl]^-{g}\ar@{}@<-1.5ex>[dl]|{\circlearrowleft}\\
C
}
\end{equation}

(29)

%(29) Case I
\begin{equation}
\xymatrix{
A\ar[rr]^-{f}\ar[dr]_-{h}&\ar@{}[d]|{\circlearrowright}&B\ar[dl]^-{g}\\
&C&
}
\end{equation}

(30)

%(30) Case II
\begin{equation}
\xymatrix{
A\ar[rr]^-{f}\ar[dr]_-{h}&\ar@{}@<0.8ex>[d]|{\circlearrowright}&B\ar[dl]^-{g}\\
&C&
}
\end{equation}

(31)

%(31) Case III
\begin{equation}
\xymatrix{
A\ar[rr]^-{f}\ar[dr]_-{h}&&B\ar[dl]^-{g}\\
&C\ar@{}[u]|{\circlearrowright}&
}
\end{equation}

(32)

%(32) 3番目の配置
\begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar[rd]_-{h}\ar@{}@<2.0ex>[rd]|{\circlearrowright}&B\ar[d]^-{g}\\
&C
}
\end{equation}

(33)

%(33) 4番目の配置
\begin{equation}
\xymatrix{
&B\ar[dr]^-{g}\ar@{}[d]|{\circlearrowright}&\\
A\ar[ru]^-{f}\ar[rr]_-{h}&&C
}
\end{equation}

(34)

%(34) 四角形の可換図式 (i)
\begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar[d]_-{h}\ar@{}[rd]|{\circlearrowright}&B\ar[d]^-{g}\\
C\ar[r]_-{i}&D
}
\end{equation}

(36)

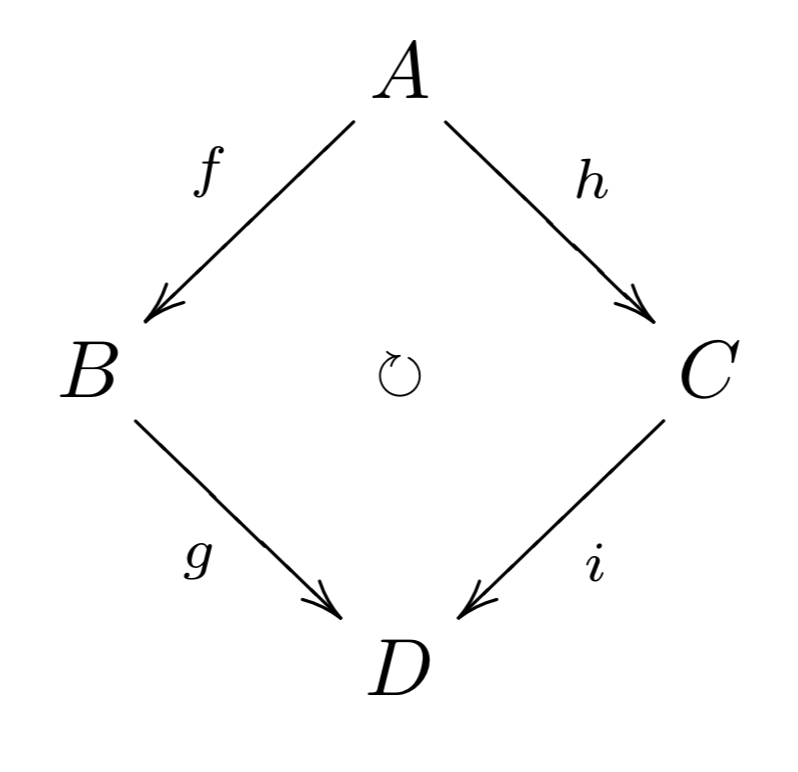
%(36) 四角形の可換図式 (ii)
\begin{equation}
\xymatrix{
&A\ar[ld]_-{f}\ar[rd]^-{h}\ar@{}[dd]|{\circlearrowright}&\\
B\ar[dr]_-{g}&&C\ar[dl]^-{i}\\
&D&
}
\end{equation}

(37)

%(37) 恒等射の法則(The Identity Laws)
\begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar[d]_-{1_A}\ar[rd]|f\ar@{}@<2.5ex>[rd]|{\circlearrowright}\ar@{}@<-2.5ex>[rd]|{\circlearrowleft}&B\ar[d]^-{1_B}\\
A\ar[r]_-{f}&B
}
\end{equation}

(38)

%(38) モノイダル圏における五角形公理
\begin{equation}
\xymatrix{
&&(A\otimes B)\otimes (C\otimes D)\ar[rrdd]^-{\alpha_{A, B, C\otimes D}}&&\\\\
((A\otimes B)\otimes C)\otimes D\ar[rruu]^-{\alpha_{A\otimes B, C, D}}\ar[dd]_-{\alpha_{A, B, C}\otimes 1_{D}}\ar@{}[rrrrd]|{\circlearrowright}&&&&A\otimes ((B\otimes C)\otimes D)\\
&&&&\\
(A\otimes (B\otimes C))\otimes D\ar[rrrr]_-{\alpha_{A, B\otimes C, D}}&&&&A\otimes ((B\otimes C)\otimes D)\ar[uu]_-{1_A\otimes \alpha_{B, C, D}}
}
\end{equation}

(39)

%(39) モノイド対象における五角形公理
\begin{equation}
\xymatrix{
&M\otimes(M\otimes M)\ar[rd]^-{1_M\otimes \mu}&\\
(M\otimes M)\otimes M\ar[ru]^-{\alpha_{M, M, M}}\ar[d]_-{\mu\otimes 1_{M}}\ar@{}[rr]|-{\circlearrowright}&&M\otimes M\ar[d]^-{\mu}\\
M\otimes M\ar[rr]_-{\mu}&&M
}
\end{equation}

Part III
(40)

%(40): 終対象(Terminal Objects) と 始対象(Initial Objects)
An object $T$ in a category $\textbf{C}$ is called a \textit{terminal object} if for any object $A$ in $\textbf{C}$ there is a unique arrow from $A$ to $T$. Dually an object $I$ in $\textbf{C}$ is called an \textit{initial object} if for any object $A$ in $\textbf{C}$ there is a unique arrow from $I$ to $A$.

\begin{align}
&\xymatrix{
A\ar@{.>}[r]^-{t_A}&T
}
&
\xymatrix{
I\ar@{.>}[r]^-{i_A}&A
}
\end{align}

(41)

%(41): 積(Products)
Let $A$ and $B$ be objects in a category $\textbf{C}$. An object $P$ in a category $\textbf{C}$ is called a \textit{product} of $A$ and $B$ if there are arrows $A\overset{p_A}{\leftarrow}P\overset{p_B}{\to}B$ such that for any pair of arrows $A\overset{f}{\leftarrow}X\overset{g}{\to}B$ there is a unique arrow $\langle f, g \rangle: X\dasharrow P$ making the following diagram commutative:
\begin{equation}
\xymatrix{
&X\ar[dl]_-{f}\ar@{.>}[d]|{^{\exists !}\langle f, g \rangle}\ar[dr]^-{g}\ar@{}@<2.5ex>[ld]|{\circlearrowright}\ar@{}@<-2.5ex>[rd]|{\circlearrowleft}&\\
A&P\ar[l]^-{p_A}\ar[r]_-{p_B}&B}
\end{equation}
That is, $p_A\circ \langle f, g \rangle = f$ and $p_B\circ \langle f, g \rangle = g$.

(42)

%(42) 双対積(Coproducts)
Dually an object $Q$ in $\textbf{C}$ is called a \textit{coproduct} of $A$ and $B$ if there are arrows $A\overset{q_A}{\to}Q\overset{q_B}{\leftarrow}B$ such that for any pair of arrows $A\overset{f}{\to}X\overset{g}{\leftarrow}B$ there is a unique arrow $\langle f, g \rangle: Q\dasharrow X$ making the following diagram commutative:
\begin{equation}
\xymatrix{
&X\ar@{}@<2.5ex>[ld]|{\circlearrowleft}\ar@{}@<-2.5ex>[rd]|{\circlearrowright}&\\
A\ar[ru]^-{f}\ar[r]_-{q_A}&Q\ar@{.>}[u]|{^{\exists !}\langle f, g \rangle}&B\ar[lu]_-{g}\ar[l]^-{q_B}
}
\end{equation}
That is, $\langle f, g \rangle \circ q_A = f$ and $\langle f, g \rangle \circ q_B = g$.

(43)

%(43) イクワライザー(Equalizers)
Let $A\overset{f}{\underset{g}{\rightrightarrows}}B$ be a pair of arrows in a category $\textbf{C}$. An \textit{equalizer} of $f$ and $g$ is a pair $(E, e)$ where $E$ is an object of $\textbf{C}$ and $e: E\to A$ is an arrow in $\textbf{C}$ with the following properties:
\begin{enumerate}
\item 
$f\circ e = g\circ e$
\item For any arrow $h: X\to A$ with $f\circ h = g\circ h$ in $\textbf{C}$, there is a unique arrow $\bar{h}: X\dasharrow E$ such that $e\circ \bar{h} = h$; i.e., the diagram below commutes:
\begin{equation}
\xymatrix{
E\ar[r]^-{e}&A\ar@<0.6ex>[r]^-{f}\ar@<-0.6ex>[r]_-{g}&B\\
X\ar@{.>}[u]^-{\bar{h}}\ar[ur]_-{h}\ar@{}@<2.5ex>[ur]|{\circlearrowright}
}
\end{equation}
\end{enumerate}

(44)

%(44) コイクワライザー(Coequalizers)
Dually A \textit{coequalizer} of $f$ and $g$ is a pair $(C, c)$ where $C$ is an object in $\textbf{C}$ and $c: B\to C$ is an arrow in $\textbf{C}$ with the following properties:
\begin{enumerate}
\item $c\circ f = c\circ g$
\item For any arrow $h: B\to X$ with $h\circ f = h\circ g$ in $\textbf{C}$, there is a unique arrow $\bar{h}: C\dasharrow X$ in $\textbf{C}$ such that $\bar{h}\circ c = h$; i.e., the diagram below commutes:
\begin{equation}
\xymatrix{
A\ar@<0.6ex>[r]^-{f}\ar@<-0.6ex>[r]_-{g}&B\ar[r]^-c\ar[rd]_-{h}\ar@{}@<2.5ex>[rd]|{\circlearrowright}&C\ar@{.>}[d]^-{\bar{h}}\\
&&X
}
\end{equation}
\end{enumerate}

(45)

%(45) プルバック(Pullbacks)
Let $A\overset{f}{\to}C\overset{g}{\leftarrow}B$ be arrows in a category $\textbf{C}$. A \textit{pullback} of $f$ and $g$ is an object $P$ in $\textbf{C}$ together with arrows $A\overset{p_A}{\leftarrow}P\overset{p_B}{\to}B$ in $\textbf{C}$ satisfying the following properties:
\begin{enumerate}
\item $f\circ p_A = g\circ p_B$
\item For any pair of arrows $h: X\to A$ and $k: X\to B$ with $f\circ h = g\circ k$, there is a unique arrow $l: X\dasharrow P$ such that $p_A\circ l = h$ and $p_B\circ l = k$; namely, 
\begin{equation}
\xymatrix{
X\ar@/^10pt/[rrd]^-{k}\ar@/_10pt/[rdd]_-{h}\ar@{.>}[rd]_-{^{\exists !}l}\ar@{}@<-0.5ex>[rrd]|{\circlearrowright}\ar@{}@<-0.5ex>[rdd]|{\circlearrowright}&&\\
&P\ar[r]^-{p_B}\ar[d]_-{p_A}\ar@{}[rd]|{\circlearrowright}&B\ar[d]^-{g}\\
&A\ar[r]_-{f}&C
}
\end{equation}
\end{enumerate}
We denote a pullback $P$ of $f$ and $g$ by
\begin{equation}
\xymatrix{
P\ar[r]^-{p_B}\ar@{}[rd]|{\text{PB}}\ar[d]_-{p_A}&B\ar[d]^-{g}\\
A\ar[r]_-{f}&C
}
\end{equation}

(46)

%(46) プッシュアウト(Pushouts)
Dually a \textit{pushout} of $f$ and $g$, where $A\overset{f}{\leftarrow}C\overset{g}{\to}B$ are arrows in $\textbf{C}$, is an object $P$ in $\textbf{C}$ together with arrows $A\overset{p_A}{\to}P\overset{p_B}{\leftarrow}B$ in $\textbf{C}$ satisfying the following properties:
\begin{enumerate}
\item $p_A\circ f = p_B\circ g$
\item For any pair of arrows $h: A\to X$ and $k: B\to X$ with $h\circ f = k\circ g$, there is a unique arrow $l: P\dasharrow X$ such that $l\circ p_A = h$ and $l\circ p_B = k$. That is, the following diagram commutes:
¥begin{equation}
\xymatrix{
C\ar[r]^-{g}\ar[d]_-{f}&B\ar[d]^-{p_B}\ar@{}[ld]|{\circlearrowright}\ar@/^10pt/[rdd]^-{k}\ar@{}@<0.5ex>[rdd]|{\circlearrowright}&\\
A\ar[r]_-{p_A}\ar@/_10pt/[rrd]_{h}\ar@{}@<-0.5ex>[rrd]|{\circlearrowright}&P\ar@{.>}[rd]^-{^{\exists !}l}&\\
&&X
}
\end{equation}
\end{enumerate}
We denote a pushout $P$ of $f$ and $g$ by
\begin{equation}
\xymatrix{
C\ar[r]^-{g}\ar[d]_-{f}\ar@{}[rd]|{\text{PO}}&B\ar[d]^-{p_B}\\
A\ar[r]_-{p_A}&P
}
\end{equation}

僕から以上