どうも僕です。
Python(パイソン)を勉強し始めたので、いろいろなプログラムを書いています。今回は最大公倍数と最小公倍数を求めるプログラムを書きました。プログラムを書きながら、Pythonの使い方を勉強しています。私は数年前にC言語を少し授業で勉強したっきりの、まるっきりの素人です。一番最初には中央値を求めるプログラムを書きました。しかし、それは別の日にブログに書きます。最大公倍数はGreatest Common Divisorというので、gcdという関数で定義します。同様に、最小公倍数はLeast Common Multipleというのでlcmという関数で定義しました。例えば、 と入力すれば、
と表示される関数です。また、
と表示されます。結論から言えば、そのようなプログラムは次のようにしてできました。今回はそれを解説したいと思います。


最大公倍数と最小公倍数についての初等整数論
最大公約数と最小公倍数
まず最大公倍数と最小公倍数の知識についてまとめます。簡単のために2つの整数 についてのみ考えます。
の最大公倍数(greatest common divisor)とは
の共通の約数のうち最も大きい数のことです。例えば、
つまり
のとき、
の約数は
であり、
の約数は
であるので、このときの最大公倍数は
です。
の最大公倍数を
と書きましょう。すると、先ほどの例は
となります。
同様に、 の最小公倍数(least common multiple)とは
を約数とするような数のうち最小のものをいいます。例えば、
の最小公倍数は
です。というのも、
となり、
は
と
の約数をもつ最小の数です。ここでドット
は掛け算を表しています。
の最小公倍数を
と書きましょう。すると、
となります。
最大公倍数と最小公倍数の求め方: ユークリッド互除法
整数 の最大公約数
と最小公倍数
は次のような関係があります。
実際、 のとき、
より、
となります。
このような関係があるので、最大公倍数がわかれば最小公倍数を求めることができます。同様に、最小公倍数がわかれば最大公倍数を求めることができます。ここでは最大公倍数をユークリッド互除法と呼ばれるアルゴリズムによって求めて、それから最小公倍数を求めます。ユークリッド互除法(ごじょほう)は次のようなものです。2つの整数の大きい数を小さい数で割り、その余りがあったときは、その小さな数をその余りで割り、それが余りが0になるまでおこない、余りが0のときの割られたものがその2数の最大公約数であるというものです。
例えば、 とすると次のようになります。
(0)
(大きい数 を小さな数
で割ると、
が余りになります。)
(1)
(小さな数 を(0)の余り
で割ると、余りが
となります。)
(2)
(小さな数 を(1)の余り
で割ると、余りは
となります。)
(3) アンダーラインのある数 が求める最大公約数です。
一般的に表せば次のようになります。整数 に対して、
(0)
(1)
(2)
(k-1)
(k)
以上が最大公約数と最小公倍数を求めるプログラムに必要な数学的知識です。
Pythonのプログラムの基本知識
関数
2つの整数 に対して、最大公約数
を求める関数を定義します。そのためにまずはPythonの関数について説明します。
それは例えば次のようなものです。

これは関数 を表しています。
例えば、この関数の変数 に
を代入すると、つまり
とすると、

となり、 を返します。
ここで注意しなければならないことは、(i) コロン( : )を必ず書くことと(ii) 定義の次の行は必ず、空白を少なくとも1つは入れなければならないことです。
実際に、コロンを入れなかったり、定義の後にスペースを入れなかったら次のような、エラーが起こります。

1つめはコロン : を入れずに改行したためのエラーであり、2つめは改行した後、スペースを入れていなかったためのエラーです。
ちなみに、スペースは少なくとも1つあればいいのですが、慣習としてスペースは半角で4つのスペースが入れられます。

1つめはスペースが1つしかないもの。それでもよい。だが、慣習としてスペースは2つめのように半角で4つ開ける(開けられる)。
最後にreturnについてですが、returnがなくても関数は定義できますが、実際に の値を代入したときに、returnがないと表示されません。returnの代わりにprintというものを使っても構いません。次の写真を参照にしてください。

function1はreturnがないので、 を代入しても、計算はしているけれども、答え
が表示されません。
function2はreturnのあとに、カンマ( , )を入れることによって、答えが複数出ます。つまり であるため
が計算されたので、
という答えが表示されました。もしも、答えを縦に表示したいのならば、funtion3のようにprintを使えばいいです。returnは関数のときに使える(と思います。まだreturnはよくわかりません)。
さて、ここまでのテストでは変数は1つしか考えていませんでしたが、もちろん変数は何個でも構いません。今回使うのは の2変数です。

計算の演算は足し算だけでなくさまざまあります。次の図を参照してください。

上から順に 和()、差(
)、積(
)、商 or 割り算(
)、最後が剰余です。ここでは
の余り
を表示しています。
今回、関数 と
を定義するにあたって、積と商と剰余が使われています。
If文(条件文)
「もし~ならば、こうであり、もし~でないならば、しかじかである」というふうにしたいときは条件文(if)を使います。例えば、「もし、 が偶数ならば、EVEN(偶数)を表示して、
がそうでなければ(つまり奇数であるならば)、ODD(奇数)を表示する」という関数は次のようにできます。
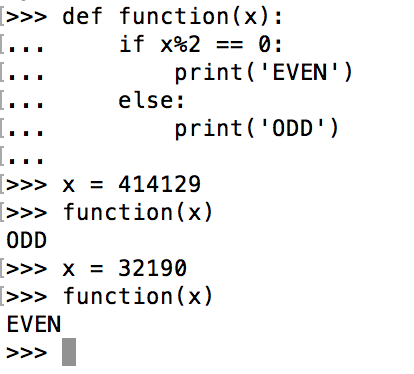
ここで「 が偶数である」というのは「
を
で割った余りが
である」ということと同じです。したがって、剰余の記号%を使っています。
ただしPythonのとき等号(イコール)は通常とは異なり、==とイコールを2つつけます。 ですので、x%2 == 0と書かれています。ノットイコール のときは、!=を使います。
While文(繰り返し文)
whileはある条件を満たすまで繰り返し計算を行うときに使われます。例えば、次のようなプログラムを考えます。

これは次のようなことが書かれています。
(I) ----
を
としろ(
を
で定義しろ)。
(II) ----
が 10より小さいならば、以下のことをせよ。
(III) ----
の二乗をせよ(pythonでは
を
で書く)。
(IV) ----
にプラス1をせよ。
(V) 繰り返し
(VI) が 10になれば止まる。
whileをさらに詳しく書くと次のようになります。
1) 初期値 は
より、
を満たす。
2) したがって、 を計算する。つまり、
である。
が表示される。
3) より初期値
に1を足す。
つまり次の初期値を
にする。
最初の を
とすると、次の初期値は
である。
4) 初期値 つまり
は
より小さい。つまり、
の条件を満たす。
5) したがって、 を計算する。つまり、
である。よって、
が表示される。
6) 初期値 に1を足す。つまり、
である。
この初期値を とすれば、
である。
7) より、
の条件を満たす。
8) したがって、 を計算する。つまり、
である。よって、
が表示される。
9) 同様に繰り返される。
10) 初期値が のとき、
を満たすので、
が計算されて表示される。
11) 初期値 に1を足す。つまり、
である。この初期値を
とおけば、
の条件
を満たさない。なぜなら、
は
より小さくないから。
12) したがって、計算は止まる。
ここで計算は上から順に行われることに注意しよう。例えば、 以降を
(1)
と書くのか
(2)
によって答えが異なってきます。実際に試してみると、次のようになります。

(2)のほうは、初期値 から次の初期値
を計算して、それから
を計算して表示されています。
もしも、 を設定しないと、初期値はずっと
であるため、
条件をいつまでも満たします。したがって、ずっと計算して無限ループをします。ですので、そのへんはしっかり確認してください。
今回の最大公約数を求めるプログラムを作る場合、大きい整数と小さい整数の剰余が でない限り、ずっと計算し続けます。そのため有限回で必ず剰余が
になるということを保障しなければなりません。前節の
の場合は2回目で----(2)----
となります。それが任意の2つの整数でも成り立つことを示さなければなりません。実際、ユークリッド互除法が有限回でストップすることは初等整数論で示されます。ですので、無限ループに陥ることはありません。
Int・Max・Min
最後に定義せずに使える特別な関数を説明します。まずはintです。これは小数に対して、その整数部分を出力する関数です。

もちろん、整数を入力したら整数が出力します。
maxおよびminは最大値と最小値を選ぶような関数です。

以上が今回プログラムで使われるPythonの基本的な知識のまとめです。
プログラムを作る
以上によって、数学的な知識とプログラムの知識をまとめました。最後にユークリッド互除法で最大公約数を求めるプログラムを定義します。最大公約数が求められたら最小公倍数も求められます。それは最初の見出しのプログラムです。このプログラムを解説します。
整数 として、最大公約数
ができているとします。このとき、最小公倍数
は
より、次のように定義することができます。

がついているのは、割り算を行なった結果、
のように小数第一位まで入ってしまうので、見やすくするために導入されています。
そこであとは最大公約数を求める関数 を定義します。
STEP 1 数の大小を決める
ユークリッド互除法をおこなうためには大きい数から小さい数を割らなければなりません。しかし、変数 はどちらが大きいか小さいかの語順は関係なく代入されます。そのため、まずはじめに
と
と定めます。以後はこの
を変数として考えます。
STEP 2 もし、 と
が割り切れるならば、
を表示させる。
今後の議論のために、もし と
が割り切れるならば、
と表示させるようにします。例えば、
であり、
のときは、割り切れるので、最大公約数は
です。ですので、
と表示させます。
STEP 3 もし、 と
が割り切れないならば、ユークリッド互除法によって、割り切れるまで繰り返す。
この箇所が一番難しいです。
まず「もし、 と
が割り切れないならば」というのは、
文の
以降のことです。つまり「もしそうでないならば」ということです。
次に「 と
が割り切れるまで繰り返す」とは「割り切れないまで以下のことを繰り返せ」ということです。つまり、
%
とします。
そして、 回目
から 回目
を求めるときは、次のように書けばいい。
%
例えば、 を考えてみましょう。
まず当然ながら%
%
です。ですので、
の条件を満たします。
と
とおいて、
以下は次の通りです。
1) %
2)
3)
4) %
かどうか調べる。
%
%
である。したがって、
条件を満たす。
5) %
6)
7)
%
かどうか調べる。すると、
であり余りは
であるから、
の条件を満たさない。
STEP 4 割り切れたならば、%
を表示する。
「割り切れたならば 」とは、ここでは「%
でないこと」つまり、
です。
このとき、%
を表示すればいいので、
とすればいいです。
以上で最大公約数のプログラムができました。
例えば、実装したら次のようになりました。

おわり
はじめてプログラムを書いてみました。少し面白いなと思いました。おそらくコンピュータ・サインエンスは「どのようなプログラムが有限回で終わるか」などを議論しているのだなと思いました。
今後もPythonでプログラムを書きます。見やすさも試行錯誤します。
追記 2018/07/19
最大公約数を求めるプログラム は次のようなものでもいい。

わざわざ 文を使わなくてもよい。その代わりに
を
ではなく、
にしなければならない(もし、
とすると、例えば
のとき、
とはならず、
%
%
が表示されてしまうからである)。
こちらのプログラムの方が少しだけだがシンプルである。 最小公倍数 は同じプログラムである。
僕から以上