可換図式をLaTeXで書くときに使うxymatrixのテンプレート (2): 2つ以上の射と可換図式の基本 - 疑念は探究の動機であり、探究の唯一の目的は信念の確定である。

今回は図式において最も使われる三角形の可換図式と四角形の可換図式のテンプレートをまとめる。さらに最後にモノイダル圏において使われる五角形の可換図式も書く。これらのコードは勝手に使って構わんよーーー。役に立ってくれたら嬉しいです。

前回の記事はこちら

追記 2018/12/01

可換図式のまとめを見やすく書いた。こちらを参照。

2つ以上の射
可換図式
終わりに

2つ以上の射

(18) 2つの射

INPUT

¥begin{equation}
\xymatrix{
A\ar[r]^-{f}&B\ar[r]^-{g}&C
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180616042430p:plain

(19) 合成射(Compositon) Case I

INPUT

¥begin{equation}
\xymatrix{
A\ar[r]^{f}\ar@/^18pt/[rr]^{h}&B\ar[r]^-{g}&C
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180616042615p:plain

(20) 合成射 Case II

INPUT

¥begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar@/^18pt/[rr]|h&B\ar[r]^-{g}&C
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180616042824p:plain

同様にして、射の文字を下につけることも可能である。下の図式を参照。

(21) 合成法則(The Composition Law)

INPUT

¥begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar@/^18pt/[rr]^-{g\circ f}&B\ar[r]^-{g}\ar@/_18pt/[rr]_-{h\circ g}&C\ar[r]^-{h}&D
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180616042934p:plain

同じドメインからコドメインへの2つの射

(22) Case I: 0.5ex

INPUT

¥begin{equation}
\xymatrix{
A\ar@<0.5ex>[r]^-{f}\ar@<-0.5ex>[r]_-{g}&B
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180616043110p:plain

(23) Case II: 0.8 ex

INPUT

¥begin{equation}
\xymatrix{
A\ar@<0.8ex>[r]^-{f}\ar@<-0.8ex>[r]_-{g}&B
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180616043542p:plain

こちらの方が射の間が開いている。

(24) 同型射(Isomorphisms)

INPUT

¥begin{equation}
\xymatrix{
A\ar@<0.5ex>[r]^-{f}&B\ar@<0.5ex>[l]^-{f^{-1}}
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180616043652p:plain

可換図式

ここでは可換図式を書く。図式が可換であるときしばしば回転射 ${\circlearrowright}$ や ${\circlearrowleft}$ が表示される。もちろん回転射を書かなくてもいいのだが、そちらのほうがそれっぽくかっこよく見える。けれども少し、めんどくさい。

可換な三角形図式

三角形の図式を作るためには3つの対象の配置は次の4パターンがある(だろう。ほかにもあるかな)。

(i)

f:id:yoheiwatanabe0606:20180617054548p:plain

(ii)

f:id:yoheiwatanabe0606:20180617054633p:plain

(iii)

f:id:yoheiwatanabe0606:20180617054708p:plain

(iv)

f:id:yoheiwatanabe0606:20180617054800p:plain

これらの対象間の可換図式を順番に書く。

(i)

(25) Case I: 1.5 ex

INPUT

¥begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar[d]_-{h}&B\ar[dl]^-{g}\ar@{}@<-1.5ex>[dl]|{\circlearrowright}\\
C
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180617051633p:plain

(26) Case II: 2.0 ex

INPUT

¥begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar[d]_-{h}&B\ar[dl]^-{g}\ar@{}@<-2.0ex>[dl]|{\circlearrowright}\\
C
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180617051739p:plain

(27) Case III: 2.5 ex

INPUT

¥begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar[d]_-{h}&B\ar[dl]^-{g}\ar@{}@<-2.5ex>[dl]|{\circlearrowright}\\
C
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180617051930p:plain

これら3つのケースを比べたら、2.0 exが一番いいのかもしれない。

(28) 別の回転射(Another cicle arrow)

INPUT

¥begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar[d]_-{h}&B\ar[dl]^-{g}\ar@{}@<-1.5ex>[dl]|{\circlearrowleft}\\
C
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180617052021p:plain

(ii)

(29) Case I

INPUT

¥begin{equation}
\xymatrix{
A\ar[rr]^-{f}\ar[dr]_-{h}&\ar@{}[d]|{\circlearrowright}&B\ar[dl]^-{g}\\
&C&
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180617052114p:plain

(30) Case II

INPUT

¥begin{equation}
\xymatrix{
A\ar[rr]^-{f}\ar[dr]_-{h}&\ar@{}@<0.8ex>[d]|{\circlearrowright}&B\ar[dl]^-{g}\\
&C&
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180617052158p:plain

(31) Case III

INPUT

¥begin{equation}
\xymatrix{
A\ar[rr]^-{f}\ar[dr]_-{h}&&B\ar[dl]^-{g}\\
&C\ar@{}[u]|{\circlearrowright}&
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180617052306p:plain

1番目と3番目は結局、回転射は同じ配置になったと思う。もう少し上にあってくれた方が嬉しいけれども、許容範囲かな。

以下の2通りは前のものとほとんど同じであるから、簡単に紹介するだけである。

(iii)

(32) 3番目の配置

INPUT

¥begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar[rd]_-{h}\ar@{}@<2.0ex>[rd]|{\circlearrowright}&B\ar[d]^-{g}\\
&C
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180617052346p:plain

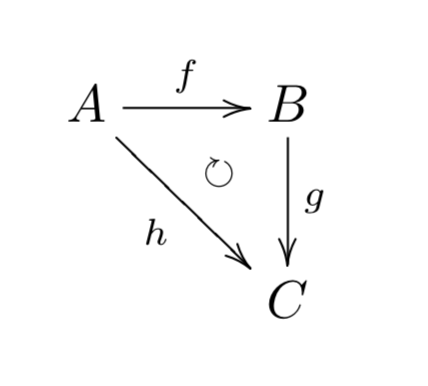
(iv)

(33) 4番目の配置

INPUT

¥begin{equation}
\xymatrix{
&B\ar[dr]^-{g}\ar@{}[d]|{\circlearrowright}&\\
A\ar[ru]^-{f}\ar[rr]_-{h}&&C
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180617052436p:plain

可換な四角形図式

次は可換な四角形の図式(commutative squares)である。

(34) 四角形の可換図式 (i)

INPUT

¥begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar[d]_-{h}\ar@{}[rd]|{\circlearrowright}&B\ar[d]^-{g}\\
C\ar[r]_-{i}&D
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180617052523p:plain

ここでひとつ注意をしておこう。回転射 ${\circlearrowright}$ を書くとき、\ar@{}[rd]|{\circlearrowright} と書かれており、@{} というのがついている。これは必要なのだろうか。答えは必要であり、もし @{} を書き忘れたら、次のように表示される。

(35)

INPUT

¥begin{equation}
\xymatrix{
A\ar[r]\ar[d]\ar[rd]|{\circlearrowright}&B\ar[d]\\
C\ar[r]&D
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180617052603p:plain

このように @{} がなければ斜めの射が表示されるのである。

(36) 四角形の可換図式 (ii)

INPUT

¥begin{equation}
\xymatrix{
&A\ar[ld]_-{f}\ar[rd]^-{h}\ar@{}[dd]|{\circlearrowright}&\\
B\ar[dr]_-{g}&&C\ar[dl]^-{i}\\
&D&
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180617052647p:plain

少し大きいし離れている。

(37) 恒等射の法則(The Identity Laws)

INPUT

¥begin{equation}
\xymatrix{
A\ar[r]^-{f}\ar[d]_-{1_A}\ar[rd]|f\ar@{}@<2.5ex>[rd]|{\circlearrowright}\ar@{}@<-2.5ex>[rd]|{\circlearrowleft}&B\ar[d]^-{1_B}\\
A\ar[r]_-{f}&B
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180617052736p:plain

可換な五角形図式

最後に五角形の可換図式(Commutative Pentagons)を2つほど書く。

(38) モノイダル圏における五角形公理

INPUT

¥begin{equation}
\xymatrix{
&&(A\otimes B)\otimes (C\otimes D)\ar[rrdd]^-{\alpha_{A, B, C\otimes D}}&&\\\\
( (A\otimes B)\otimes C)\otimes D\ar[rruu]^-{\alpha_{A\otimes B, C, D}}\ar[dd]_-{\alpha_{A, B, C}\otimes 1_{D}}\ar@{}[rrrrd]|{\circlearrowright}&&&&A\otimes ( (B\otimes C)\otimes D)\\
&&&&\\
(A\otimes (B\otimes C) )\otimes D\ar[rrrr]_-{\alpha_{A, B\otimes C, D}}&&&&A\otimes ( (B\otimes C)\otimes D)\ar[uu]_-{1_A\otimes \alpha_{B, C, D}}
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180617052857p:plain

ここでINPUTをよく見るとカッコ「(」が2回使われているところには少し隙間がある。これはブログに正しく表示されるためにそのように書いているだけであって、LaTeXに書くときは隙間はあってもなくてもいい。

(39) モノイド対象における五角形公理

INPUT

¥begin{equation}
\xymatrix{
&M\otimes(M\otimes M)\ar[rd]^-{1_M\otimes \mu}&\\
(M\otimes M)\otimes M\ar[ru]^-{\alpha_{M, M, M}}\ar[d]_-{\mu\otimes 1_{M}}\ar@{}[rr]|-{\circlearrowright}&&M\otimes M\ar[d]^-{\mu}\\
M\otimes M\ar[rr]_-{\mu}&&M
}
¥end{equation}

OUTPUT

f:id:yoheiwatanabe0606:20180617052959p:plain